| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- Java
- 앱개발
- 군간
- Eigenvector
- 조건부정리
- pintos
- Android
- AIC
- Eigenvalue
- 행렬
- Flutter
- 운영체제
- qq플롯
- 상대 엔트로피
- 선형대수학
- 비둘기집원리
- 개발자
- f비
- 최대우도법
- 알고리즘
- 군내
- 잔차
- 논리회로 #컴퓨터
- 일반화오차
- 파스칼삼각형
- 개발
- 앱
- 자바
- 평균로그우도
- ios
- Today
- Total
Dev_bob
[선형대수학]Eigenvalues and Eigenvectors 본문
Eigenvalues, Eigenvectors
A가 n*n matrix (square matirx)입니다.
λ는 scalar 값입니다.
square matrix A에 대하여 nonzero vector x에 대해
Ax= λx를 만족하는 벡터 x가 존재할 때,( λ 는 상수)
λ를 eigenvalue
x를 eigenvector 라고 합니다.
그렇다면 square matrix A가 주어졌을 때 eigenvector와 eigenvalue 값은 어떻게 구하는 지 알아봅시다.
구하는 순서는 다음과 같습니다.
1. eigenvalue 찾기
Ax= λx에서 A는 행렬, λ는 scalar값이므로 연산하기 어렵습니다. 이 점에서 양 변에 항등행렬I를 곱합니다.
AIx=Ax= λIx
Ax- λIx=0
(A- λ I)x=0 를 계산하면 됩니다.

위의 (A- λI)x=0의 x가 영벡터가 아닌 해를 가지기 위한 필요충분 조건은
Cramer정리에 의해 계수행렬의 행렬식이 0인 것입니다. 즉, det( A- λI )=0인 값을 찾아야합니다.

우리는 eigenvalue 값을 찾은 것입니다. λ 값은 7또는 2 입니다.
이제 λ=7, λ=2 값을 대입해서 해당하는 eigenvector x 값을 찾으면 됩니다.
2. eigenvector 찾기


이렇게 eigenvector 값을 구했습니다.
[2 3]^T 와 [-1 1]^T 입니다.
eigenspace는 구하기
고유공간 (eigenspace)은 행렬 와 관련된 고유값 에 대응하는 모든 고유벡터의 집합과 영벡터(0 벡터)를 포함하는 벡터 공간입니다. 구체적으로, 고유공간은 다음과 같이 정의됩니다
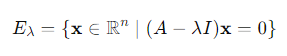
여기서:
는 고유값 에 대응하는 eigenspace입니다.
는 주어진 행렬입니다.
는 고유값입니다.
는 단위행렬입니다.
는 고유벡터입니다.
이제 eigenvector와 eigenvalue의 기하학적 의미를 살펴봅시다.
Ax= λx 를 해석해보자면
square matrixA와 벡터 x를 곱한 값이 상수와 벡터x를 곱한 값과 같다는 것입니다.
즉, 행렬의 곱의 결과가 원래 벡터x와 방향은 같고 배율만 상수 λ만큼 비례해서 변했다는 의미입니다.

형광펜이 쳐진 부분을 보시면,
Ax에서 x는 앞서 구한 eigenvector들의 선형조합으로 나타낼수 있으므로, 다음과 같이 표시합니다.
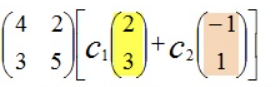
이때 행렬 A를 x에 곱하게 되면 결과는

이렇게 되는데요, 이것이 의미하는 바는 행렬 A를 곱했을 때 방향은 동일하고, 배율만 7배,2배만큼 변했다는 것을 의미합니다.

"λ 는 eigenvalue of A이다."
-> Ax= λx를 만족하는 0이 아닌 벡터가 존재한다
->(A- λI)x=0 은 nontrivial solution이다
->null(A- λI)x=0 은 nontrivial 하다.
-> (A- λI)는 nonivertible하다.
참고자료
https://rfriend.tistory.com/181
[선형대수] 고유값(eigenvalue), 고유벡터(eigenvector) 의 정의
지난번 포스팅에서는 행 사다리꼴(Row echelon form)과 계수(Rank)를 이용해서 선형연립방정식 해의 존재성(existence)과 유일성(uniqueness)을 알아보는 방법을 소개하였습니다. 이번 포스팅에서는 고유값(
rfriend.tistory.com
